A Numerical Solution of Second-Order Linear Boundary Value Problems Using Natural Cubic Splines

Abstract

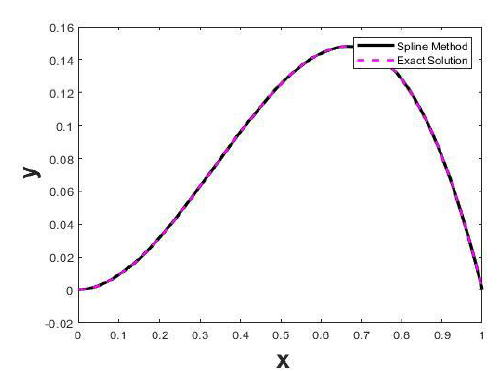
In this paper, a natural cubic spline method (NCS) has been developed to solve two-point boundary vale problems (BVPS) of second order1 differential equation. The solution of the BVPs is initially approximated by cubic splines and derived a recurrence relation with natural spline constraints. Replacing this recurrence relation and respective cubic spline approximation in BVPs, obtained a tri-diagonal system of equation. An efficient Thomas algorithm is used to find the solution and represents the results graphically. The famous differential equations from Bessel’s equation, Lane-Emden equation, porous catalyst pellet has been considered to check the developed NCS method. Table values for various step sizes are computed in order to verify the developed method’s accuracy. The outcomes are contrasted with those obtained using the shooting technique and spectral methods as well as with those found in the literature.