Natural Cubic Spline for Parabolic Equation with Constant and Variable Coefficients

Abstract

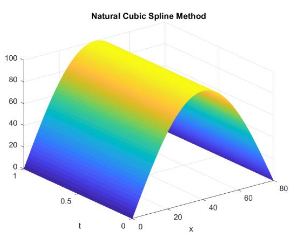
This research tackles solving a broad class of second-order partial differential equations (PDEs) with a novel method using natural cubic splines. These equations, crucial in science and engineering, describe phenomena like heat flow and wave propagation. The method works for both parabolic (diffusion) and hyperbolic (wave) equations, with a focus here on parabolic ones. The key idea lies in approximating the spatial derivatives in the PDE with the second derivative of a natural cubic spline function. Imagine a smooth curve broken into segments; natural cubic splines ensure these segments connect seamlessly while having zero second derivative at the joints. This makes them ideal for mimicking the solution's behavior. For the time derivatives, the paper employs a finite difference method. This approximates the derivative based on the function's values at specific time steps. By combining these approximations, the original PDE transforms into a system of solvable algebraic equations. The paper explores solving this system explicitly (directly calculating new solutions based on previous ones) and implicitly (solving a system of equations at each step). This offers flexibility, with explicit schemes being faster but potentially less stable, while implicit schemes provide more stability but require more computation. Finally, the paper validates the method's effectiveness through numerical examples with various boundary conditions (specifying the solution's behavior at domain edges). This showcases the method's applicability in real-world scenarios with different constraints. In conclusion, this research offers a valuable tool for solving diverse second-order PDEs. The method's ability to handle both constant and variable coefficients and its exploration of different solution strategies make it a versatile and adaptable approach.